In this post we’re going to use fastai to solve the Titanic passenger survival prediction problem on Kaggle.
Titanic passenger survival
In this prediction problem, we’re given descriptions of Titanic passengers, along with their survival outcome (survived vs died). Based on this, we need to train a machine learning model that is later evaluated on another passenger data file, where the survival outcomes are hidden (Kaggle knows them, but we don’t).
The training file (first few lines):
| PassengerId | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | Survived |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.25 | S | 0 | |
| 2 | 1 | Cumings, Mrs. John Bradley | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C | 1 |
| 3 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.925 | S | 1 | |
| 4 | 1 | Futrelle, Mrs. Jacques Heath | female | 35.0 | 1 | 0 | 113803 | 53.1 | C123 | S | 1 |
| 5 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.05 | S | 0 | |
| 6 | 3 | Moran, Mr. James | male | 0 | 0 | 330877 | 8.4583 | Q | 0 | ||
| 7 | 1 | McCarthy, Mr. Timothy J | male | 54.0 | 0 | 0 | 17463 | 51.8625 | E46 | S | 0 |
| 8 | 3 | Palsson, Master. Gosta Leonard | male | 2.0 | 3 | 1 | 349909 | 21.075 | S | 0 | |
| 9 | 3 | Johnson, Mrs. Oscar W | female | 27.0 | 0 | 2 | 347742 | 11.1333 | S | 1 | |
| 10 | 2 | Nasser, Mrs. Nicholas | female | 14.0 | 1 | 0 | 237736 | 30.0708 | C | 1 |
fastai
We’re going to use fastai .
fastai a high-level deep learning library providing ready-to-use neural network architectures for a number of common problem types. The downside of using such library is that we don’t get to learn all the fascinating details of how neural networks are designed and trained. The upside is that we get a working solution in no time.

Behind the scenes, fastai uses the popular PyTorch library. So overall our techs stack will look like this:
- 🤖 fastai: high-level deep learning library providing ready-to-use neural network architectures
- 🔥 PyTorch low-level deep learning library. It provides an optimized framework for defining and running neural networks
- 💻 Hardware The actual CPU and GPU on the computer
Tabular learner
fastai comes with ready-to-go neural network architectures for common classes of problems. One of these classes is for making predictions based on tabular data, which is exactly what we need for the Titanic competition.

To use the Tabular learner, we need to feed it the passenger data. The framework can handle two types of features:
- continuous: where the value of the feature is a number on some numeric scale. For example: age, ticket price
- categorical: where the values represent some abstract categories that are not part of numeric scale. For example: port of embarkation, ticket class, sex
There’s no obvious way of handling opaque features such as ticket number, passenger name or cabin number, so we’re going to simply ignore it. Let’s see some code! The train.csv data file comes from Kaggle.
import pandas as pd
df = pd.read_csv('../input/titanic/train.csv')
# Drop the opaque features we're going to ignore
df = df.drop(['Name', 'Cabin', 'Ticket'], axis=1)
df.columnsThis produces the list of the remaining features: ['PassengerId', 'Survived', 'Pclass', 'Sex', 'Age', 'SibSp', 'Parch', 'Fare', 'Embarked']. Let’s configure the tabular learner indicating which are continuous, which are categorical, and which is the variable we learn how to predict.
from fastai.tabular.all import *
splits = RandomSplitter(valid_pct=0.2)(range_of(df))
to = TabularPandas(df, procs=[Categorify, FillMissing, Normalize],
cat_names = ['Pclass', 'Sex', 'Embarked'],
cont_names = ['Age', 'Fare', 'SibSp', 'Parch'],
y_names='Survived',
y_block=CategoryBlock,
splits=splits)fastai takes care of preprocessing:
FillMissingreplaces missing data points with averages/most common values for each feature. This way we don’t have to discard an entire passenger if we’re missing an entry for one of their featuresNormalizescales continuous variables, so that they fit the range of 0.0 to 1.0. This helps the neural network train better (bigger numbers tend to grow too much when they’re multiplied together).Categorifyhandles categorical variables using embeddings, more on this below
Peeking inside the box
To use the Tabular learner, we don’t need to understand the neural network behind it. But it’s instructive to take a peek!
dls = to.dataloaders(bs=64)
learn = tabular_learner(dls, metrics=accuracy)
print(learn.model)This prints out a detailed description of the underlying PyTorch neural network that fastai set up:
TabularModel(
(embeds): ModuleList(
(0): Embedding(4, 3)
(1): Embedding(3, 3)
(2): Embedding(4, 3)
(3): Embedding(3, 3)
)
(emb_drop): Dropout(p=0.0, inplace=False)
(bn_cont): BatchNorm1d(4, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(layers): Sequential(
(0): LinBnDrop(
(0): Linear(in_features=16, out_features=200, bias=False)
(1): ReLU(inplace=True)
(2): BatchNorm1d(200, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(1): LinBnDrop(
(0): Linear(in_features=200, out_features=100, bias=False)
(1): ReLU(inplace=True)
(2): BatchNorm1d(100, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
(2): LinBnDrop(
(0): Linear(in_features=100, out_features=2, bias=True)
)
)
)Let’s look at the main pieces:
The four “embedding” modules. These are needed for each “categorical” variable in our input: sex, point of embarkation, class, etc. Embeddings represent each category as an abstract vector of numbers, allowing the model to learn hidden relations between category elements. For example, if people who embarked in Southampton had similar survival outcomes to those who embarked in Cherbourg, but different than those in Queenstown, the model will be able to learn that.
Linear modules. Linear(in_features=16, out_features=200) is the core of the network. Here the 16 input attributes of each passengers are connected to 200 artificial neurons: mathematical formulas that will try to learn relations between data points and their survival outcomes. We also have a second layer of these, connecting 200 neurons in layer 1 with 100 neurons in layer 2.
Output. At the end, the last linear layer connects the 100 neurons in layer 2 to just 2 output features, corresponding to two survival outcomes: survived or perished.
With the neural network in place, we need just one more line of code to train it on the training data:
learn.fit_one_cycle(20)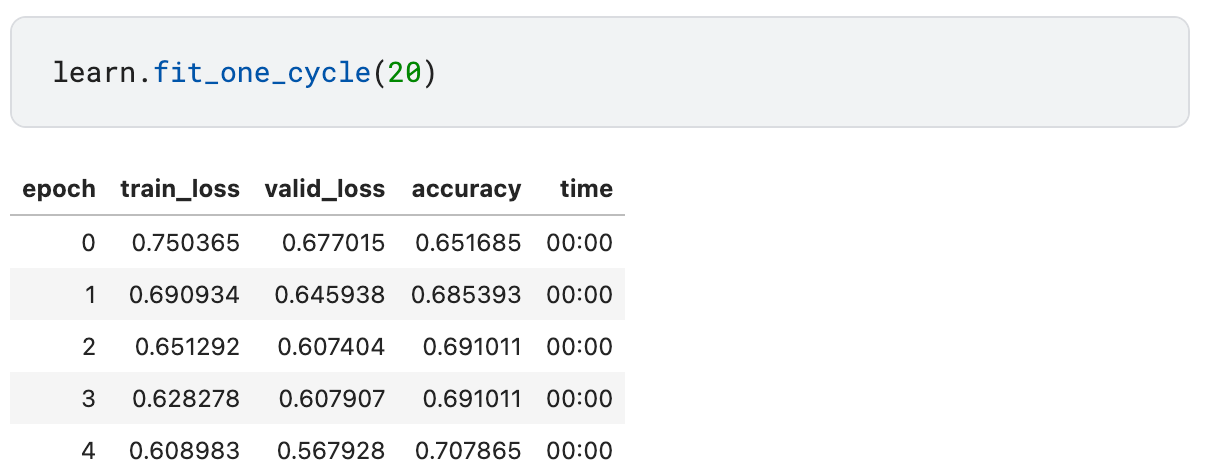
Results
When submitted on Kaggle, the fastai neural network solution reaches the accuracy of 78% out of the box.

This is much better than the baseline 62% for a solution that simply predicts that everyone dies and a bit better than 76% I got a few months back when experimenting with decision forests. Not bad!
Conclusion
With a high-level framework like fastai, it’s easy to train a neural network for a specific problem using one of the built-in architectures. These can be used as black boxes, but we can also peek at the underlying neural network architecture to understand how it works. In either case, rapid prototyping can be very helpful regardless of our expertise level, as it allows us to quickly try and compare different solutions.
Happy training!